 链表中环的入口结点
链表中环的入口结点
# 23. 链表中环的入口结点
# 题目描述
一个链表中包含环,请找出该链表的环的入口结点。要求不能使用额外的空间。
# 解题思路
使用双指针,一个快指针 fast 每次移动两个节点,一个慢指针 slow 每次移动一个节点。因为存在环,所以两个指针必定相遇在环中的某个节点上。
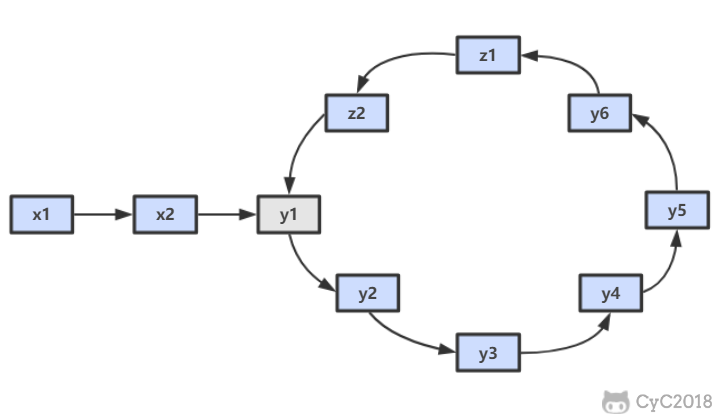
假设环入口节点为 y1,相遇所在节点为 z1。
假设快指针 fast 在圈内绕了 N 圈,则总路径长度为 x+Ny+(N-1)z。z 为 (N-1) 倍是因为快慢指针最后已经在 z1 节点相遇了,后面就不需要再走了。
而慢指针 slow 总路径长度为 x+y。
因为快指针是慢指针的两倍,因此 x+Ny+(N-1)z = 2(x+y)。
我们要找的是环入口节点 y1,也可以看成寻找长度 x 的值,因此我们先将上面的等值分解为和 x 有关:x=(N-2)y+(N-1)z。
上面的等值没有很强的规律,但是我们可以发现 y+z 就是圆环的总长度,因此我们将上面的等式再分解:x=(N-2)(y+z)+z。这个等式左边是从起点x1 到环入口节点 y1 的长度,而右边是在圆环中走过 (N-2) 圈,再从相遇点 z1 再走过长度为 z 的长度。此时我们可以发现如果让两个指针同时从起点 x1 和相遇点 z1 开始,每次只走过一个距离,那么最后他们会在环入口节点相遇。
public ListNode EntryNodeOfLoop(ListNode pHead) {
if (pHead == null || pHead.next == null)
return null;
ListNode slow = pHead, fast = pHead;
do {
fast = fast.next.next;
slow = slow.next;
} while (slow != fast);
fast = pHead;
while (slow != fast) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
上次更新: 2022/08/01, 18:47:48
